GeometryThinking

garnermath.com

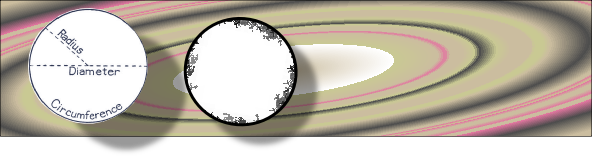
π = C/d

x2 + y2 = r2

Geometry Thinking

A Two Component View of How Geometric Thinking Works

Component #1: Abstract vs. Concrete Thinking. Sometimes students (and their teachers) have difficult transitions from Algebra 1 to Geometry.

The difficulty begins with how we start problem solving in each type of math. Algebra usually begins in the imagination with variables and formulas (the abstract); Geometry begins with what we can see and touch (the concrete).

Now this doesn’t seem like much difference, but it is a big one. Algebra begins with the abstract, like formulas and variables, where you constantly draw upon your imagination to remember that letters represent numbers. Geometry deals with the concrete visual pictures of points, lines, planes, angles, polygons and circles, before any formula is put on paper. And although geometry formulas are algebraic, thought begins with a picture of the figure before we begin to reach for any formulas.

Early grade school began with visual pictures of numbers. We learned about the number 3 by seeing pictures of 3 sticks, 3 cats, 3 dogs, etc. We even learned arithmetic through pictures; we might have learned 3+4=7 by seeing a picture of 3 apples and another 4 apples grouped to make 7 apples.

Soon, our numbers got bigger; we worked with numbers in the hundreds, thousands and millions. Because these numbers are too big to draw and count up, pictures get abandoned for algorithms. Algorithms are those steps we use from memory to: add and multiply large numbers by carrying digits, or learn subtraction and division through borrowing digits.

Because our late grade school and junior high years are heavily weighted developing arithmetic, pre-algebra and algebra thinking, we can get into a 6+ year rut of one way of thinking - that is remember/imagine a formula or algorithm which matches the problem, and move on to ‘solve’ it.

In geometry thinking, we go BACK to the way we approached math in early grade school - we go back to looking at pictures first. In geometry as a high school teen, we are drawing on brain cells and thinking patterns which haven’t been used in years, unless we are big into art, design, building or tinkering.

So, to be successful in geometry, we have to break an old habit of how we approach math - that old habit of beginning with imagination and equations, and going straight to the answer, rarely drawing a picture.

Our new habit for successful geometry requires us to begin with a right understanding of a what we SEE, BEFORE we ever bring any algebra into it.

Component #2: Logic and Reasoning. In addition to the visual aspects, there’s a logic component to geometry which is a challenge whether a person is a concrete/visual learner or abstract learner.

There are 3 undefinded terms, a host of definitions, and a handful of laws which belong to the world of geometry. How we combine them creates the rules or postulates allowing us to use geometry; this combination process is the logic and reasoning component to geometry.

The legal and medical professions constantly draw upon the logic and reasoning processes of geometry. Research and analysis in science and engineering are also dependent upon these same processes developed within geometry. And how much improvement could business, government and personnel management be improved through applying logic?

The flowchart below shows typical ups and downs associated with the logic and reasoning found within geometry. You can actually see the complexity of thought which resides in geometry. You don’t just think ‘forwards’ like in algebra; you have to think ‘forwards’ and ‘backwards’ until you get to your solution. This is why just being a visual learner is not enough to be good at geometry; it requires learning to think clearly and logically with purpose.

The consequences of not learning geometric processes may lock up a student’s math effectiveness for a long time. Even if we’re good at math, all of our math knowledge won’t do us much good if we look at something and can’t relate it to any of the arithmetic, algebra, geometry, or calculus we may know.

A Flowchart of Geometry Thinking